Context:
My experiments with Javascript – The Bulls and Cows Game
The bulls and cows game
I started off writing the Bulls and Cows game just to pass time when I am bored, but soon it turned out to be an interesting mathematical problem. Also thanks to
I continued my experiments yesterday. I started off by writing a small function that analyzes the already entered numbers and gives the list of possible numbers that can match all the criteria (in the previously entered numbers) and be a possible solution. This was supposed to be a hint to the user.
I saw that the list of possible solutions diminishes as the user enters more and more numbers (this is quite obvious, but I want to make it clear). In order to assist the user to select the next number, I created a weighted system (explained later) that gives the user the most probable solution.
This finally led to the simulation of an environment, where player 'A' thinks of a number and player 'B' tries to guess it, both player 'A' and 'B' being computer controlled. (Computers are so dumb that a single program can contain both player 'A' and 'B' without them knowing about each other 🙂 )
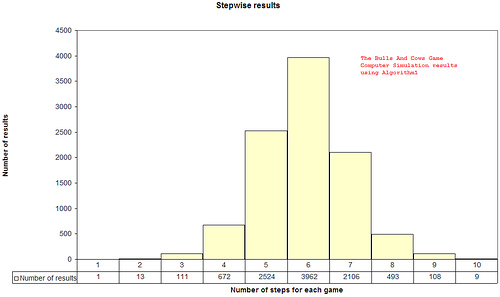
I ran the simulation for each and every possible number (1 to 9999) and guess what? With some tweaks, the computer is able to find the solution in an average of 6 steps. The maximum steps it requires is 10.
Here is a graph showing the result:
The algorithm that I wrote is as follows:
1. Player 'A' thinks of a number.
2. Player 'B' starts of with number 1234 as the first try and player 'A' responds with the number of bulls and cows in the number. (I haven't tried other numbers, but I guess it will give similar results)
3. Player 'B' tries to find out the set of solutions that can match each of the previous steps.
4. 'B' then finds out how many times each digit occurs in the list of possible solutions. These form the weights of the digits.
5. Using this, 'B' computes a weight for each possible solution as folows:
If 'abcd' is a possible solution and the digits 'a','b','c','d' have weights 'p','q','r','s' respectively, then weight of 'abcd' is 'p'+'q'+'r'+'s', such that 'a','b','c','d' are distinct. If they are not distinct, then each digit is considered only once to compute the weight -> (This is the tweak I had to apply).
6. 'B' then finds the number with the highest weight and uses this as the next step.
7. Repeat Steps 3 – 6 until you get the solution.
I ran this simulation for all the numbers from 1 – 9999 and got the following results:
Algorithm 1 result sheet.
It took me about 20 minutes to run the simulation in my system (an average of about 10 games per second).
I am not sure if this is the best solution, but there are learnings from this:
* It is possible for a computer to find out a solution in an average of 6 steps or less.
* The maximum number of steps required to arrive at a solution is 10 or less.
Please note that the algorithm was not tested (i.e. I am not sure if it works exactly as I have mentioned it here), but the answers it provides and the steps have been authenticated.
Is there any better solution?